問題
問3
図の木構造は2分探索木である。a～gの値の大小関係として、適切なものはどれか。ここで、a～gの値は重複しないものとする。
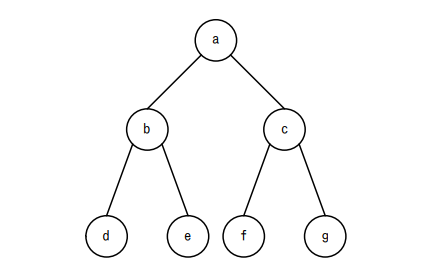
- a ＜ b ＜ d ＜ e ＜ c ＜ f ＜ g
- d ＜ b ＜ e ＜ a ＜ f ＜ c ＜ g
- d ＜ e ＜ f ＜ g ＜ b ＜ c ＜ a
- g ＜ f ＜ c ＜ e ＜ d ＜ b ＜ a
[出典：基本情報技術者試験 令和7年度(科目A) 問3]
正解
正解は「イ」です。
解説
正解は「イ」です。この問題は「2分探索木（Binary Search Tree）」の基本的な性質を理解しているかを問うものです。2分探索木とは、あるノードに対して「左の子にはそれより小さい値」「右の子にはそれより大きい値」が入るという規則を持つ木構造です。
図が示す2分探索木に従って、a～gのノードの値の大小関係を読み取る必要があります。まず、根のノードaが中心で、左側にb・d・e、右側にc・f・gがあります。aより左のノードはすべてaより小さく、aより右のノードはすべてaより大きい必要があります。さらに、左側・右側のノード内でも、それぞれの部分木に対して同様のルールが適用されます。
この条件を図に合わせて整理すると、d ＜ b ＜ e ＜ a ＜ f ＜ c ＜ g の順で並べられることが分かります。これが選択肢「イ」に該当します。問題は図の構造を視覚的に正しく読み取り、大小関係をツリー構造に基づいて推論できるかが鍵となります。
例えば、bの左にdがあるということは、d ＜ b、bの右にeがあるので、b ＜ e。また、bはaの左なので、e ＜ a。aの右にはcがあり、cの左にfがあるので、a ＜ f ＜ c。cの右にgがあるため、c ＜ g。これをすべてつなげると、d ＜ b ＜ e ＜ a ＜ f ＜ c ＜ g となり、選択肢イが正しいことが分かります。
ア(a ＜ b ＜ d ＜ e ＜ c ＜ f ＜ g):
aの左にあるはずのdやeがbより後ろに来ており、ツリー構造の規則に反しています。
ウ(d ＜ e ＜ f ＜ g ＜ b ＜ c ＜ a):
bがgよりも後ろに来ていますが、gはaの最も右下のノードで、aより大きいためこの並びは不適切です。
エ(g ＜ f ＜ c ＜ e ＜ d ＜ b ＜ a):
全体的に逆順で、aより右側にあるgやfが左に来ているなど、2分探索木の規則に反します。
難易度
この問題の難易度は「やや難しい」です。2分探索木というデータ構造の定義自体は基本的ですが、図からノードの関係を正しく読み取り、大小関係として並べ替える能力が求められます。特に視覚的な構造を正しく把握することが難しいと感じる初学者にとっては、ややハードルが高い問題です。
用語補足
2分探索木（Binary Search Tree）：
各ノードに最大2つの子ノードを持ち、「左の子＜親＜右の子」というルールで構成される木構造です。検索や追加・削除の操作を高速に行える特徴があります。
ノード：
木構造における1つ1つの点を指します。例えば「a」「b」「c」などの値が入っている箱のようなもので、親子関係によって全体の構造が決まります。
木構造：
根（ルート）から枝分かれして下に伸びる階層構造です。家系図や組織図のような関係性を示すのに使われることが多く、プログラミングやデータ管理において重要な概念です。
解法のポイント
2分探索木の構造的特徴（左が小さい、右が大きい）をしっかり覚えましょう。図から値の大小関係を推測する練習問題を繰り返し解くことで視覚的な判断力も身につきます。加えて、ツリー構造に関する用語（ノード、葉、部分木など）も整理しておくと応用問題にも対応できます。
