問題
問1
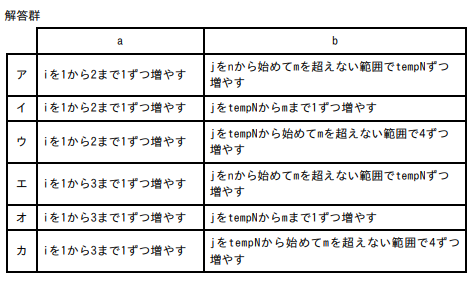
次のプログラム中の【 a 】と【 b 】に入れる正しい答えの組合せを、解答群の中から選べ。
関数function1が受け取る引数と、関数function2が受け取る引数が同じとき、二つの関数は同じ値を返す。ここで、引数nと引数mは正の整数であり、引数mは引数nよりも10以上大きい数とする。

[出典:基本情報技術者試験 令和7年度(科目B) 問1]
正解
正解は「カ」です。
解説
この問題のポイントはfunction1とfunction2が同じ値を返すことから、どちらも「nからmまでの範囲で4の倍数を数える処理」をしていると理解することです。function1は直接nからmまでループして4の倍数を数えています。一方function2は少し工夫した別の方法で同じカウントを得ています。
【a】はtempN(=n)を条件判定に使っているループです。tempNが4の倍数になるまでtempNをインクリメントするループであり、最小限の繰り返しで終了する必要があります。選択肢の「iを1から3まで1ずつ増やす」が最適です。理由は、4の倍数になるまで最大3回(例:1→2→3→4)で到達できるからです。
【b】は4の倍数に到達した後、その倍数からmまでcountを数えるループです。function1では「iをnからmまで1ずつ増やす」のと同じ処理が必要なので、「jをtempNから始めてmを超えない範囲で4ずつ増やす」が正解です。なぜなら、すでにtempNは4の倍数であり、次以降も4ずつ進めば次の4の倍数を漏れなくカウントできるからです。
以上から、正解は「カ」となります。
ア(iを1から2まで…):
tempNが4の倍数になるまで最大3回必要なため、2回のループでは十分でなく、場合によって4の倍数になる前に終了してしまいます。
イ(jをtempNからmまで1ずつ増やす):
1ずつ増やしては4の倍数だけをカウントする効率的な処理にならず、function1の動きと一致しません。
ウ(jをtempNから始めてmを超えない範囲で4ずつ増やす):
aのループ条件が不適切(iを1から2まで)なためtempNが正しい4の倍数で終了しないケースが生じます。
エ(iを1から3まで…):
aは適切ですが、bでtempNずつ増やしているため、4の倍数ごとにカウントできず処理が正しく行われません。
オ(jをtempNからmまで1ずつ増やす):
bの条件で1ずつ増やしてしまうため、4の倍数のみをカウントする効率性と一致しません。
難易度
この問題の難易度は「やや難しい」です。function1とfunction2が同じ結果を返す前提を活用し、2つのコード構造を比較する力が求められるからです。またtempNのループや4の倍数処理の仕組みをしっかり理解しているかで正解率が大きく変わります。
用語補足
![]() mod(剰余演算):
mod(剰余演算):
割り算をして余りを求める演算です。例えば7 mod 4は3になります。プログラムでは特定の倍数かどうかを判定する際によく使われます。
![]() for文:
for文:
繰り返し処理を行うための構文です。「iを1から3まで1ずつ増やす」という形でループの開始と終了、増やし方を指定できます。日常で言えば「1階から3階まで1階ずつ階段を上る」ような動きです。
![]() カウント処理:
カウント処理:
条件に一致した回数を数える処理です。count変数を使って特定の条件が満たされるたびに「1」を加えることで実現します。例えば、お祭りで来場者数を数えるのと同じイメージです。
解法のポイント
for文やmod演算など基本的な制御構文と演算の動きを実際にコードを書いて練習することが重要です。特に「条件分岐と繰り返しの組み合わせ」については、図解などで視覚的に理解するのも有効です。関数同士の結果一致を求める問題にも慣れておきましょう。





